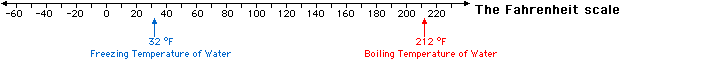An interval scale is a scale (of measurement) created by units of equal size.

When dealing with an interval scale, the difference between any two values can be calculated by using subtraction.

Ratios of values have no meaning, because the value of zero is arbitrary.

Some examples of variables that use interval scales would be time, temperature (Celsius), temperature (Fahrenheit), etc.

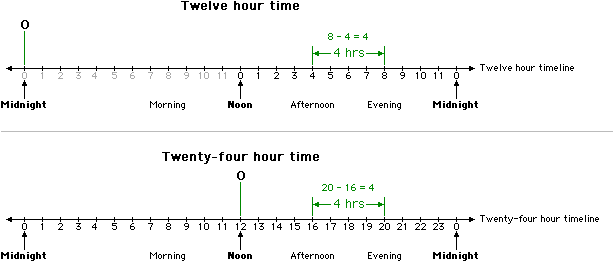
When using a twelve hour clock, we can compare the time of 4:00 in the afternoon to 8:00 in the evening. It is possible to say that the difference in time is four hours (8:00 − 4:00). Please see the illustration below.

On a comparable twenty-four hour clock, we can compare the time of 16:00 in the afternoon to 20:00 in the evening. It is possible to say that the difference in time is four hours (20:00 − 16:00). Please see the illustration above.

If we look at the ratios of these numbers [4/2 = 2, and 18/16 = 1.125], the ratios are different, indicating that these ratios have no meaning.

The Celsius scale is "created" by setting the freezing point of water to 0 and the boiling point of water to 100 (a difference of 100). Please see the illustration below.

The Fahrenheit scale is "created" by setting the freezing point of water to 32 and the boiling point of water to 212 (a difference of 180). Please see the illustration below.

Compare the scales by putting them together.

Equal differences in any two temperatures on one scale will result in equal differences on the other scale.

• 10 °C is equivalent to 50 °F
• 30 °C is equivalent to 86 °F
• 40 °C is equivalent to 104 °F
• 60 °C is equivalent to 140 °F

Note that 30 °C - 10 °C = 60 °C - 40 °C (both are a difference of 20 °C).

Note that 86 °F - 50 °F = 140 °F - 104 °F (both are a difference of 36 °F).

A difference of 20 °C is equivalent to a difference of 36 °F, regardless of where you are on either scale.

Although 30 x 2 = 60 and 30 °C x 2 = 60 °C, it is meaningless (incorrect) to state that 60 °C is twice as hot as 30 °C.

• 30 °C is equivalent to 86 °F
• 60 °C is equivalent to 140 °F

60 °C is twice the numerical value of 30 °C, but when we look at these Celsius values converted to Fahrenheit values, there is a contradiction [we would expect that 86 °F x 2 = 140 °F, but 86 x 2 ≠ 140 (the ratio 140/86 is approxamately 1.63)

It can be stated that the difference between 140 °F and 32 °F is double the difference between 86 °F and 32 °F (54 x 2 = 108), since 32 °F is eqivalent to "ZERO" on the Celsius scale.

This example used the "zero" of the Celsius scale. Similar results occur if the zero of the Fahrenheit scale is used.

The Celsius and Fahrenheit scales are interval scales because the location of zero on each scale is arbitrary. For a temperature scale to be a ratio scale, zero must NOT be arbitrary. If zero is defined as the temperature where molecular motion stops (absolute zero), then a ratio scale for temperature can be defined.

The Kelvin temperature scale defines zero (0 K) this way. Absolute zero is -273.15 °C or -459.67 °F. A one degree difference in Kelvin is equal to a one degree difference in Celsius. A chart showing the formulas to change between Kelvin and Celsius as well as Kelvin and Fahrenheit is given below.

The three temperature scales are shown below.

Twice as hot on the Kelvin scale has meaning since the location of zero is not arbitrary.

If it is desired to know how how hot it is if it is twice as hot as 30 °C, change 30 °C to Kelvin [303.15 K], double the numerical value in Kelvin [606.3 K], then change the result to Celsius [333.15 °C]. Please see the illustration below.